1. ホーム
少しでも分かりやすく伝えたい2の補数

皆さんこんにちは！！
今回は2の補数について解説したいと思います！

2の補数とは

2の補数とは、加算のみで減算を行う為に必要な値であり、それを用いることで減算を行うことができます。
加算のみで減算するなんて、初めて2の補数に触れる方にとって意味不明な文ですよね。私も何を言っているのか分からなくなりそうなのでその仕組みを説明…とその前に2の補数の変換方法について説明していきます。
続きが知りたい方はこの後の文章を読み進めていただいて下の「2の補数の計算」で説明します。

1の補数への変換方法

「何故2の補数の記事なのに1の補数の話を始めるんだ！」なんて思う方もいるかもしれませんが、2の補数に変換を行うにはまず1の補数に変換する必要があります。
とはいっても1の補数の変換方法はとてもシンプルです！
例として下のような値を基に1の補数の変換と次の2の補数の変換を行っていきます。

この値から1の補数にする方法は、ズバリ「1」のところは「0」に「0」のところは「1」に入れ替えるだけです。

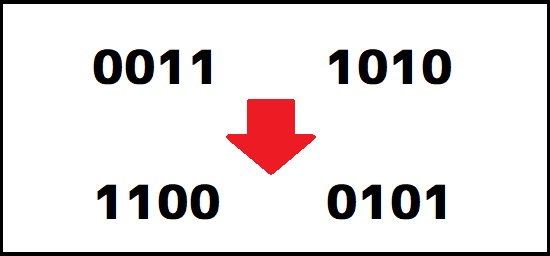
そう、ただこれだけなんです。
これで1の補数への変換が完了しました。

2の補数への変換方法

実は2の補数の変換方法もかなり単純です。
先ほど変換した1の補数に「1」を足し合わせるだけで、2の補数に変換することができます！

「1100 0101」に「1」を足し合わせると「1100 0110」になります。
たったこれだけです。
よって最初の値「0011 1010」を2の補数に変換すると「1100 0110」になります。
これで2の補数への変換は終了です。

2の補数の計算

実際に2の補数を用いた計算を行っていきます。
例として、

という2進数の式を基に説明していきます。
まずは比較として普通に減算を行います。

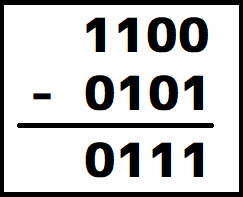
このように減算した結果は「0111」となります。
では次に2の補数を用いた減算を行っていきます。
まず減算をする「0101」を2の補数の変換していきます。
変換を行うと、「1011」となりますね。
この後は「1100」と「1011」を加算していきます。

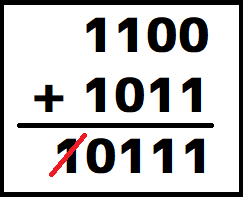
繰り上がりの桁は無視します。何故無視するのかは同記事「繰り上がりを無視する理由」について説明します。
繰り上がりを無視した結果は「0111」となります。
これは最初に「-」を用いて減算をした値と同じになりますね。

※ちなみに、今回の場合「0111」なので最上位の値が「0」なので何の問題もないですが、これが減算を行った結果最上位の桁が「1」である場合は値が「-」になります。例えば、2の補数を用いて減算を行った結果が「1100」だったとします。こういった時は2の補数に変換した処理と全く同じ処理を行います。そうすると「0100」となり10進数で直すと「-4」となります。

繰り上がりを無視する理由

何故繰り上がりを無視するのかについて説明していきます。
これは通常の減算から2の補数に分解する過程を見ていきながら説明していきます。
先ほど用いた

を基に説明していきます。
1の補数に変換するにあたって「0101」を「1010」にするには1111 – 0101 = 1010のように「1111」から変更前の値を引くことで1の補数に変更することができます。
ここから「1」を足し合わせれば2の補数になりますね。
これをまとめると、

このことから、10000を除外すると、2の補数を用いても減算になっていることが分かると思います。

何故2の補数を用いる必要があるか

ここまで長く説明して、結局「何故2の補数を用いる必要があるのか」について説明します。
今回、減算を加算のみで行ったわけですが、これをする理由はコンピュータが減算を行うより、加算を行う方が得意だからです。
細かく言うと長くなってしまうので割愛しますが、減算を加算で行うことで減算用の回路をわざわざ使う必要もなくなり、ハードウェアの構造がシンプルになるからです。

まとめ

重要なことは「0」と「1」を入れ替えた値に「1」を足す。
これを行うことで2の補数に変換することができます。