少しでも分かりやすく伝えたいボゴソート

皆さんこんにちは!!
今回は効率が非常に悪いとされるボゴソートについて説明していきます。
ボゴソートとは
ボゴソートとは何ぞやということですが、 ボゴソートとはランダムに要素を並べそれが並んでいなければ再度ランダムに要素を並べまた比べるというものすごく効率の悪いソートのことを言います。
ランダムに要素を並べるので、重複してしまう場合もあります。
極端な話、永遠にソートされない可能性すらあります。
アルゴリズム
Pythonを用いて実際にボゴソートを再現しました。
今回作成したコードはGitHubに投稿しているので、よければそちらもご覧ください。
GitHubの方にコードは乗っていますが、一応このページにも載せておきます。
今回用いたコードはこちら↓
import random
#ソートする配列とカウンター初期値の設定
a = [3, 5, 2, 1, 4]
counter = 0
#メイン処理
while True:
if a == sorted(a):
break
random.shuffle(a)
counter += 1
print(a)
print(f"試行回数{counter}回")仕組みとしてはとてもシンプルで、
ソートする配列を用意し(今回は変数aに配列を格納)それがソート済みの配列(今回だと[1, 2, 3, 4, 5]になる)と値が同じになるまでランダムに要素を並べ替え続けるというものです。
※追加で並べ替えた回数をカウントする変数counterを用意しました。
実行結果
今回の実験結果は以下の通りになりました。

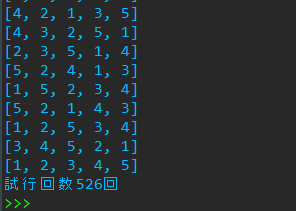
画像のように8回で終わることもあれば526回かかることもありました。
ちなみに、他の桁数で実行した場合の出力結果例は以下の通りになりました。(値は毎回変わります。)
| 桁数 | 試行回数(回) |
| 1 | 0 |
| 2 | 3 |
| 3 | 10 |
| 4 | 39 |
| 5 | 258 |
| 6 | 1119 |
| 7 | 14261 |
| 8 | 108563 |
| 9 | 634213 |
| 10 | 10543847 |
実際に動かしてみると、桁によってかなり値が変化していますね。
勿論、良し悪しはあるとは思いますが桁が多いほど試行回数が増える傾向にはあるようです。
これについては、桁数が減ればその分ソートされた配列と完全一致する確率は上がるので試行回数は少なり、逆に桁数が増えれば一致する確率は減るので試行回数はかなり増えるという理由があるためです。
まとめ
今回はボゴソートについて説明してきました。
正直使う機会はないとは思いますが、こういうソートもあるんだ程度に頭に入れておけばいつかは役立つかも(?)しれませんね。