少しでも分かりやすく伝えたい論理式の簡単化

皆さんこんにちは!!
今回は論理式の簡単化について解説したいと思います!
論理式の簡単化の仕組み
論理式の簡単化にあたって、法則がありそれらを当てはめることによって論理式の簡単化を行います。
その法則をこれから画像と共に解説していきます。
論理式の簡単化の法則
前提としてAやBは入力がHighかLow、つまり1か0しかないので、それを前提に見ていってください。
また、「論理演算」と「集合演算」の2種類を写真に載せていますが両方とも同じ意味なので片方の意味さえ分かっていただければ問題ないです。
べき等則

まずはべき等則についてです。
Aが1の時は、1*1=1、1+1=1(High)で
Aが0の時は、0*0=0、0+0=0となり、
入力した値と同じ値が出力されています。この結果からも出力がA(入力値と同じ値)であることが分かります。
交換の法則

次に交換の法則についてです。
A*B=B*Aといっても「1*0=0*1」がそれぞれ「0」になることやや「1*1=1*1」がそれぞれ「1」になったりと同じことを言っているので「=(等号)」が成り立つ事が分かります。
A+B=B+Aも同様で、「0+0=0+0」が「1」になり、
「1+0=0+1」が「1」となるので結果は同じになります。
結合の法則

次に結合の法則についてです。
Aに「1」を、Bに「0」を、Cに「1」を式に代入していきます。
最初の式「(A・B)・C = A・(B・C)」に代入していくと、
「(1 * 0) * 1 = 1 * (0 * 1)」となり両辺とも計算結果は「0」になります。
2つ目の式「(A + B) + C = A + (B + C)」に代入していくと、
「(1 + 0) + 1 = 1 + (0 + 1)」となり両辺とも計算結果は「1」になります。
他の数字を入れてみても両辺が同じ値になることから、この「結合の法則」も成り立っていることが分かります。
分配の法則

次に分配の法則についてです。
長くなってきましたが頑張りましょう!
これも「結合の法則」と同様に値を代入して説明していきます。
Aに「0」を、Bに「1」を、Cに「1」を入れていきます。
最初の式「A・(B + C) = (A・B) + (A・C)」に代入していくと、
「0 * (1 + 1) = (0 * 1) + (0 * 1)」となり両辺とも計算結果は「0」になります。
2つ目の式「A + (B・C) = (A + B)・(A + C)」に代入していくと、
「0 + (1 * 1) = (0 + 1)・(0 + 1)」となり両辺とも計算結果は「1」になります。
他の数字を入れてみても両辺が同じ値になることから、この「結合の法則」も成り立っていることが分かります。
吸収の法則

次に吸収の法則についてです。
これも実際に値を代入して説明していきます。
Aに「1」を、Bに「0」を入れていきます。
最初の式「A + (A・B) = A」に代入していくと、
「1 + (1 * 0) = 1」となり、Aの入力値と出力値が同じ値になっていることが分かります。
2つ目の式「A・(A + B) = A」に代入していくと、
「1 * (1 + 0) = 1」となり、Aの入力値と出力値が同じ値になっていることが分かります。
他の数字を入れてみても両辺が同じ値になることから、この「結合の法則」も成り立っていることが分かります。
ド・モルガンの法則

次にド・モルガンの法則についてです。
他の法則と違って学校の数学などであまり見かけないものなので、より詳しく説明をしていきます。
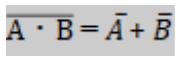
まずは両辺の上についている線について説明していきます。
線の意味は否定(Not)を示しています。このNotは値を反転する効果を持っていて、直前の結果が「1」ならば「0」に、「0」ならば「1」になるものです。
符号の上にこの記号がついているかいないかの違いについてですが、計算した結果を否定(Not)するのか否定(Not)した値を計算するのかの違いです。
文だけでは伝わりづらいと思うので、実際に値を代入していきます。
Aに「1」を、Bに「0」を入れていきます。
最初の式の左辺「A・B」を単純に計算していくと「1 * 0 = 0」となり「0」が出力されます。しかし否定(Not)があるので出力された「0」を反転します。そうすると出力は「0」から「1」になりますね。次に最初の式の右辺「A + B」を計算していきますが、今回は全体に否定(Not)が入っているのではなくそれぞれの入力値「A」と「B」に否定(Not)が入っています。この時は、最後に値を反転するのではなく最初に値を反転します。そうすると入力値が元々Aが「1」、Bが「0」だったのが反転することによってAが「0」、Bが「1」になります。あとは反転した値を「+」で取るだけなので、「0 + 1 = 1」となり、出力は「1」になります。これで、
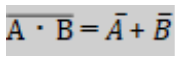
が成り立つことが分かります。
2つ目の式も同様に計算していくと同じ値が出力されます。
その他

最後に上記以外の法則です。
Aが出力されている式は、Aの入力値と出力値が同じ値になります。
「1」が出力されている式は、Aにどの値が入っても出力結果が「1」になります。
「0」が出力されている式は、Aにどの値が入っても出力結果が「0」になります。
論理式の簡単化をする理由
簡単化する理由は何と言っても式が簡略化され見やすくなることです。
例として下の画像を見てください。

吸収の法則をそのまま持ってきただけですが、例題1と例題2はどちらも結果はAで「1」となります。
同じ意味を表す式でも例題1の方が分量も少なく、パッと見ただけで値がどうなるか分かると思います。機械からしても計算する回数が少なくなるので、簡単化することでより早く値を求めることができるようになります。
まとめ
法則を見て様々な値を入れ、等式が成り立っていることを体感してください。
法則の中身だけ覚えるよりも仕組みを覚えた方が記憶にも残りやすくなります!