少しでも分かりやすく伝えたいグリーディ法

皆さんこんにちは!!
今回は近似アルゴリズムの一つであるグリーディ法について説明していきたいと思います!
グリーディ法とは
グリーディ法は英語だと「greedy algorithm」と書き、日本語だと「貪欲法」とか「欲張り法」なんて言われています。
「なんか別の言い方なかったのか…」なんて言いたくなるような名前ですが、まあそれは置いておいて。
グリーディ法はその段階で取り得る選択肢の中で一番良い選択をし続けるアルゴリズムのことです。
グリーディ法の例
では実際にグリーディ法を用いた例を説明していきたいと思います!
今回は例題として、「100円、50円、10円の硬貨が十分にあり、170円にするのに最小の枚数になるにはどの組み合わせが良いか」といったような問題があったとします。
前述したように、グリーディ法はその段階で取り得る選択肢の中で一番良い選択をし続けるアルゴリズムなので、今回の場合だと100円が最も良い選択肢になります。
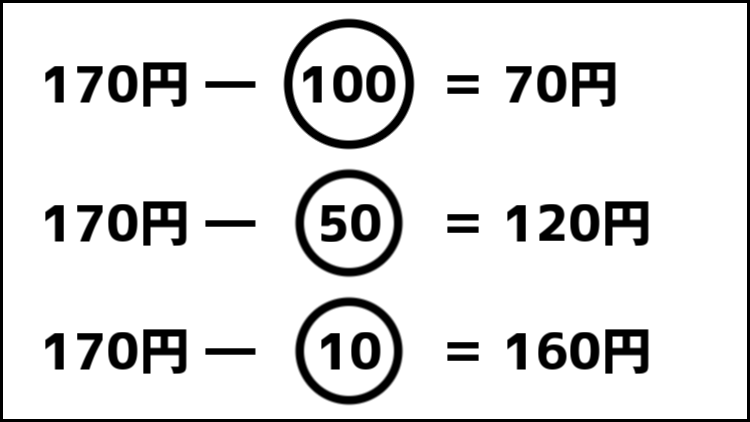
画像の通りですね。硬貨の枚数を最小にしたいので100を選択するのが最も選択肢としては適しています。
残りの70円分も同様に選択していくと、
100円:1枚
50円:1枚
10円:2枚
のようになります。
今回だとこれが最も枚数が少なく170円揃えることができます。
最適解が常に求められる訳ではない
例に挙げた問題では最適解が求まりましたが、これが例えば「100円、70円、10円の硬貨が十分にあり、140円にするのに最小の枚数になるにはどの組み合わせが良いか」になった場合はどうでしょうか。
同じようにやっていくと、
100円:1枚
70円:0枚
10円:4枚
となりますが、これは残念ながら最適解ではありません。
70円:2枚
が2枚で140円揃えることができるのでこちらが最適解になります。
これが常に最適解を得ることが出来ない一例です。
何故使うのか
必ず最適解が求まらないのに何故用いられるのかについてですが、
- 問題によっては最適解が求めることが出来る
- 最適解でなくても近似値は求めることが出来る
といった理由があります。
また、処理過程も比較的単純な構造で実装も簡単なことからこのグリーディ法が用いられています。
まとめ
今回は「グリーディ法」について説明してきました。
グリーディ法は、全ての問題において最適解は求められないがある程度の近似値が求められる、「一番良い選択をし続ける」近似アルゴリズムです!