少しでも分かりやすく伝えたいカルノー図

皆さんこんにちは!!
今回はカルノー図について解説したいと思います!
カルノー図とは
図を用いて論理式を簡単化する方法です。
モーリス・カルノーにより発明されました。
カルノー図による簡単化
まず、ここでは2変数から5変数について説明していきます。
6変数以降もありますが、5変数の場合の応用なので今回は省略させていただきます。
簡単化の方法は図の中の「1」である部分をとにかく大きく囲う事です。大きく囲うといっても囲むことができるのは、2,4,8,16個の長方形または正方形で、重ねて囲うことは出来ますがいびつな形で囲うことは出来ません。また、表の上下左右は繋がっているので、まとめて囲うことができます。
実際に囲んでいる例
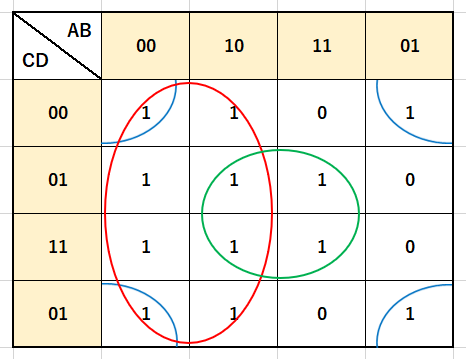
この時、2桁の入力値が00,01,11,10となっているのは、円で囲みやすくなるためです。
これが00,01,10,11等のようになると2ビット分変わっている場所ができ、円で囲みづらくなるためです。
2変数のカルノー図による簡単化
今回は下の式を基に説明を行っていきます。
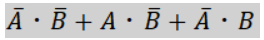
2変数、つまり変数が2つの時には2*2の表を作り簡単化を行っていきます。
まず、式の分解を行います。
極端に言えば、「+」が来るたびに分解を行えばよく、
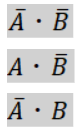
と、最初の式をこの3つの式に分けることができます。
そして、下の図のような2*2のマスを作ります。
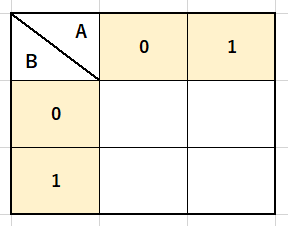
この図に分解した式をあてはめていきます。
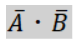
この式は「A」と「B」の両方にNotがついているので、「A」が「0」かつ「B」が「0」の場所に「1」が付きます。
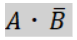
この式は「B」にNotがついているので、「A」が「1」かつ「B」が「0」の場所に「1」が付きます。
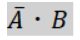
この式は「A」にNotがついているので、「A」が「0」かつ「B」が「1」の場所に「1」が付きます。
これらの式を上の図にあてはめたものが下の図になります。
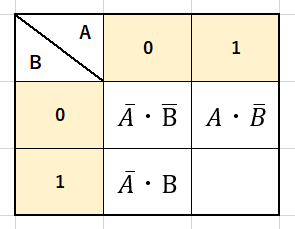
ここで式が入ったセルに「1」を、そうでない場所に「0」を入力します。
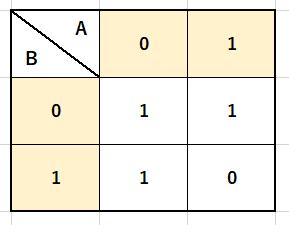
「1」である部分を全て囲います。今回は2個の長方形で囲むことができます。
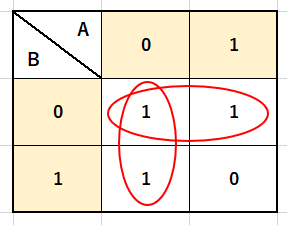
まずは横方向で囲んだ円について見ていきます。
囲んだ円の式の整理を行うと、
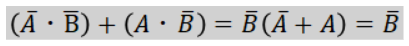
となります。この時、
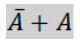
は必ず「1」となるので省略します。
次に縦方向で囲んだ円について見ていきます。
囲んだ式の整理を行うと、
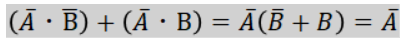
あとはそれぞれ出た結果を「+」で足し合わせるだけなので最終的に簡単化した結果は、
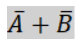
となります。
3変数のカルノー図による簡単化
次に3変数のカルノー図による簡単化を行います。
例としてこの式を用いて説明していきます。
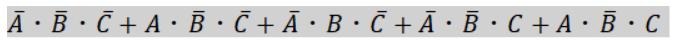
今回は2*4の表を用いて簡単化を行います。

この式を2変数の時同様分解してあてはめた結果がこうなります。
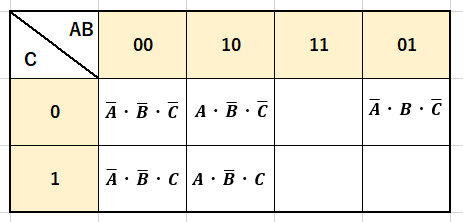
式の部分を「1」に置き換えて、囲った結果が下の図になります。
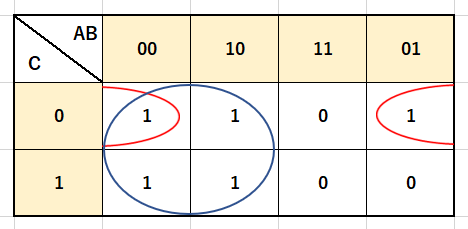
まずは、赤色で囲んだ円について見ていきます。
囲んだ円の式の整理を行うと、
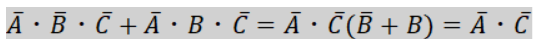
次に青色で囲んだ円について見ていきます。
囲んだ式の整理を行うと、
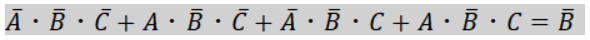
途中式を省略しましたが値が囲んだ中で値変化しない、つまり今回の場合だと
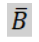
のみが残るわけです。(NotB以外は値が「0」でも「1」でも構わない)これが大きく囲う最も大きなメリットで、大きく囲うほど式が簡単化しやすくなります。
あとはそれぞれ出た結果を「+」で足し合わせるだけなので最終的に簡単化した結果は、
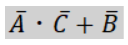
となります。
4変数のカルノー図による簡単化
次に4変数のカルノー図による簡単化を行います。
例としてこの式を用いて説明していきます。
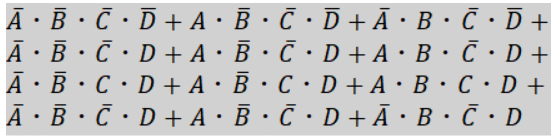
かなり長い式になりましたが、これもカルノー図を用いることで簡単化できます。
今回は4*4の表を用いて簡単化を行います。
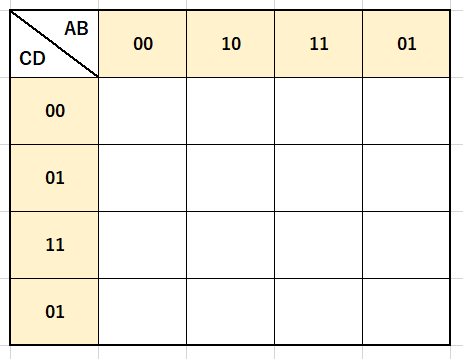
3進数の時と同様に式をあてはめ、あてはめた部分を「1」に置き換えて、囲った結果が下の図になります。

まずは、赤色で囲んだ円について見ていきます。
囲んだ円の式の整理を行うと、
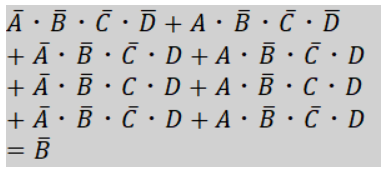
次に青色で囲んだ円について見ていきます。
囲んだ式の整理を行うと、
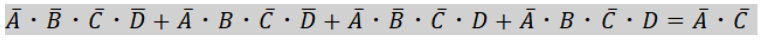
次に緑色で囲んだ円について見ていきます。
囲んだ式の整理を行うと、
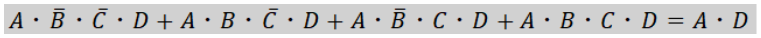
あとはそれぞれ出た結果を「+」で足し合わせるだけなので最終的に簡単化した結果は、
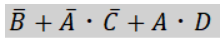
となります。
5変数以上の場合
5変数以降は、4変数の応用で解くことができます。
例えば5変数についてですが、4変数の表を2つ用いることで簡単化を行うことができます。
図で表すならばこうなります。
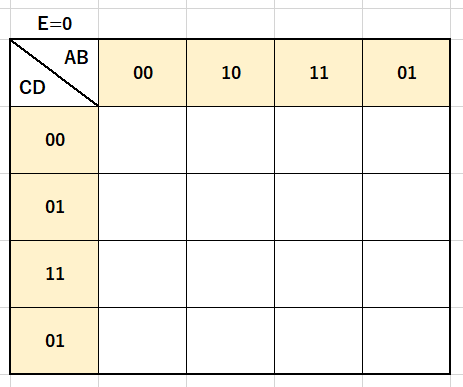
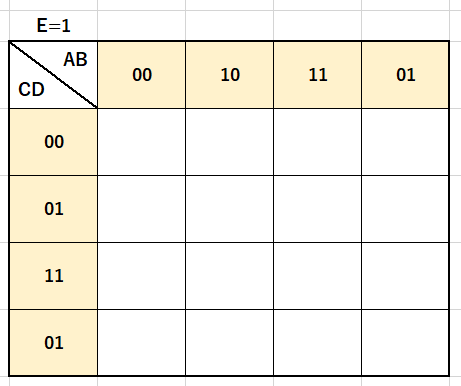
「E」の値が「0」のパターンと「1」のパターンとで場合分けすれば良いわけです。
これが6変数の場合なら4変数の表を4つ用いることで簡単化を行うことができ、「E」が「0」で「F」が「1」などのようにして場合分けをすることで簡単化ができるようになります。
カルノー図を用いるメリット
図を用いて簡単化を行うので視覚的に簡単化をしているのが分かりやすい点です。
また、短時間で簡単化を行うことができる点もカルノー図で簡単化を行う上で便利な点です。
まとめ
2,4,8,16のように2の累乗数で囲み、囲んだ円の中で簡略化することです。
5変数以降は4変数の時の応用で簡単化を行うことができます!