少しでも分かりやすく伝えたいn進数から10進数への変換

皆さんこんにちは!!
今回は様々な進数の変換方法について説明していきたいと思います!
↑過去に上の記事を書いたのですが、この方法では他の進数の時に対応できません。
ということで今回はどの進数でも一発で10進数に変換出来る方法の解説になります!
今回の変換の仕組み
結論からになりますが、
n進数で各桁の値をsとするとき、
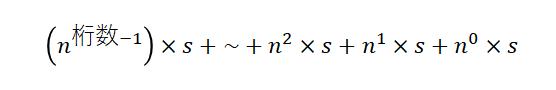
のように表すことができます。
例えば10進数で「132」という数字があったとしましょう。
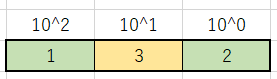
画像の通り、「132」という数字は、
というように分けられます。計算すると 100 + 30 + 2です。これを他の進数に対応させるというのが今回の方法になります。
まず10進数というのは「0~9」まで1桁で表し「9」の次は桁が増えて「10」となりますね。
「10進数だと桁が一つ増えるごとに値が10倍になる」ということです。
これが2進数なら桁が一つ増えるごとに値が2倍,3進数なら3倍という風になるのです。
この仕組みをもとに実際に進数の変換をしていきましょう。
変換してみる
では実際に3,4進数から10進数を試してみましょう。
3進数から10進数への変換
ではまず3進数から10進数の変換です。
今回は、
という3進数を基に変換していきます。
この値を桁ごとに分けていきます。
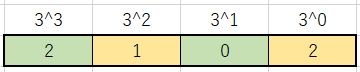
そうすると上の画像のようになりますね。
桁の上にある 3^3 や 3^2 は「今回の変換の仕組み」にあるように桁が上がると値がn倍(進数倍)されるため「上の数字 * 下の数字」を求め、各桁の値を合計することで10進数にしたときの値を求めることができます。
今回の値なら、
3^3 * 2 + 3^2 * 1 + 3^1 * 0 + 3^0 * 2
=54 + 9 + 0 + 2
=65
よって3進数の 2102 を10進数に変更すると、10進数で 65 となります。
4進数から10進数への変換
次に4進数から10進数の変換です。
今回は、
という4進数を基に変換していきます。
とは言ってもやることは3進数の時と変わりません。
この値も桁ごとに分けていきます。
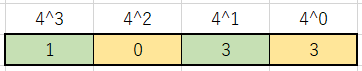
そうすると上の画像のようになりますね。
またまた同じように計算すると、
4^3 * 1 + 4^2 * 0 + 4^1 * 3 + 4^0 * 3
=64 + 0 + 12 + 3
=79
よって4進数の 1033 を10進数に変更すると、10進数で 79 となります。
まとめ
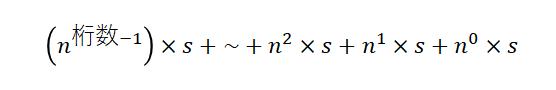
上記の式でn進数から10進数へ変換することができます!
ぱっと見ややこしそうですが仕組みは単純なのでぜひ試してみてください!