少しでも分かりやすく伝えたい逆ポーランド記法

皆さんこんにちは!!
今回は逆ポーランド記法について解説したいと思います!
逆ポーランド記法とは
逆ポーランド記法とは「1+2」の様な式があったとき、演算子(+)を後ろに、被演算子(1,2)を前に表記する記法で、別名後置記法とも言います。
ちなみに、逆ポーランド記法はコンパイラ等で用います。
逆ポーランド記法の表現方法
例として、
(3+2)*(10-2)という式があったとき、まずカッコ内を逆ポーランド記法に変換していきます。この時、普通の計算と同じ優先度で変換していくので、まずは括弧内から変換していきます。
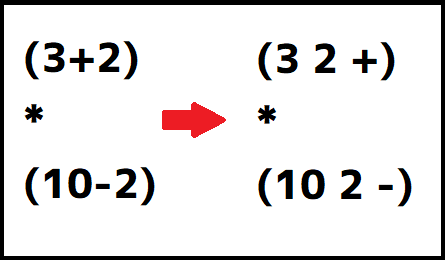
括弧内まで図の様に変換することができますね。
この後が最も重要です。
変換した「(3 2 +)」と「(10 2 -)」を何かしらの変数に置き換えます。今回は「(3 2 +)」を「A」に、「(10 2 -)」を「B」と置き換えて行きます。
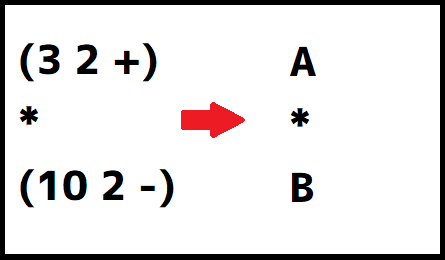
置き換えて出来た「A*B」を最初と同様に逆ポーランド記法に変換していくと「A B *」となります。
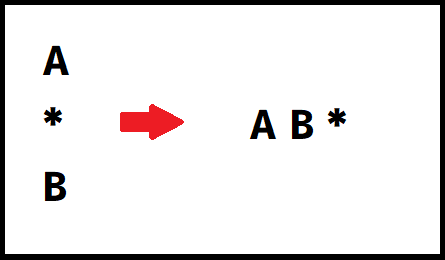
最後に置き換えた「A」と「B」を元に戻します。
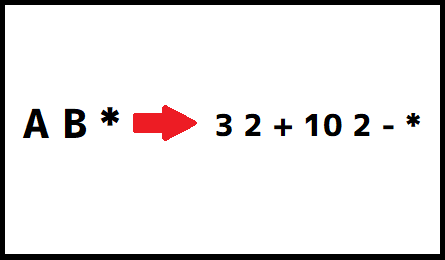
これで逆ポーランド記法に変換することができました。
逆ポーランド記法の計算方法
今回は上記で用いた「(3+2)*(10-2)」という式を基にして計算していきます。
ポーランド記法を用いずに計算を行っていくと、
(3+2)=5、(10-2)=8、5*8=40となり、計算結果は40となりますね。
次に逆ポーランド記法で計算していきます。
ここでの考え方として重要なのはスタックに当てはめて計算していくことです。
大まかな計算方法としては、
数字の時は常にスタック
↓
演算子が来たらスタックされている数値をその演算子で計算する
↓
計算した結果をスタック
↓
次の演算子が来るまでスタック
これを繰り返すだけです。
上記で変換した式と同じ式なので逆ポーランドの手順は省略しますが、「(3+2)*(10-2)」を変換すると「3 2 + 10 2 – *」となります。
「3」と「2」は被演算子なのでそのままスタックします。

「3」と「2」がスタックされた後、「+」が入りますが、演算子が来た場合はスタックされた2つの被演算子で計算を行うため「3+2=5」となり、計算結果の「5」がスタックされます。

次は「10」と「2」がスタックされます。演算子もないのでそのままスタックされます。

次に「-」が来るので直前の2つの被演算子「10」と「2」を減算し、「10-2=8」となり計算結果の「8」がスタックされます。

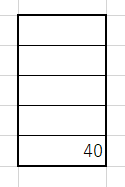
最後に「*」が来るので今までと同様計算を行い、「5*8=40」となり結果が40と分かります。
逆ポーランド記法をするメリット
逆ポーランド記法をすることによるメリットはコンピュータで計算する上で非常に便利だからです。
計算方法も演算子が来るまでは値をスタックし、演算子が来たら演算を行いその結果をスタックするだけなので計算手順も簡易的で処理が行いやすいからです。
まとめ
演算子(+,-,*,/)は後ろ、被演算子(1,2,3,4,5,6,7,8,9,0)は前において括弧でくくられていたら何かしらの変数に置き換える。
これさえできれば、逆ポーランド記法は問題なく変換することができます!